第2種電気工事士学科試験問題シリーズ(3)
皆さんこんにちは!タンです。
今日は令和5年度上期一般問題を続けます。
問題4:

解答:
この問題は、抵抗だけでなく、リアクタンスに関する問題です。
回路の消費電力とは抵抗で消費電力です、Q(J):
$$ Q =UIt(J) $$
1秒で消費電力とはP(W)です。
$$ P = \frac{Q}{t} =UI (W) $$
U:抵抗両端電圧(V)
I:抵抗に流れる電流(A)
問題より、U=100(V),I=4(A)
ので、
$$ P = UI = 100x4 = 400(W) $$
解答
ロ です。
一言:
普段の回路電力の表はP=U・I・cos(Φ)、cos(Φ):力率ですが、この回路では、並列回路ですので、cos(Φ)は無視してもいいです。
つぎ、問題5:
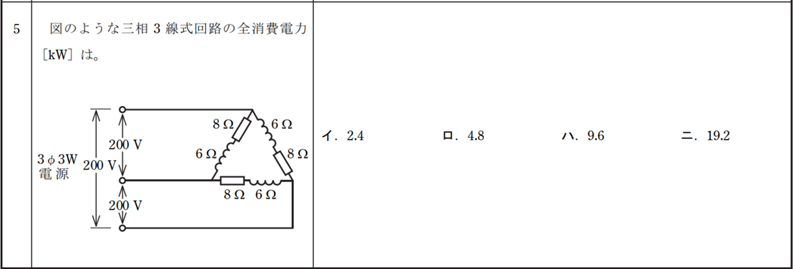
解答:
この問題はやや難しいですので、ゆっくり解決いたします。
負荷の配線方はデルタ(Δ)ですので、線間電圧(Ul)と相電圧(Up)とは等しいです。
三つの負荷は同じですので、一つ計算してから、3倍になったらいいです。
右の図面通りです。
抵抗とリアクタンスと直列繋がりますので、直列回路です。
回路の電力表は
$$ P = I^2R(W) (1) $$
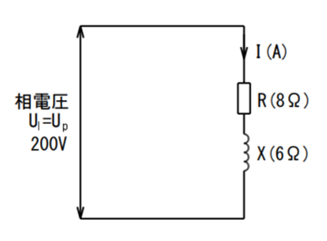
問題により、
R =8(Ω),X=6(Ω)
ので、
$$ Z = \sqrt{R^2 + X^2} = \sqrt{8^2 + 6^2} =10(Ω) $$
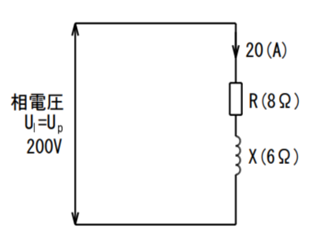
回路に流れる電流値は:
$$ I = \frac{U}{Z} = \frac{200}{10} =20(A) $$
直列回路ですので、抵抗に流れる電流(IR)=回路に流れる電流(I)です。
それで、一つ負荷での回路電力は
$$ P = I^2R = 20^2\times8 = 3200(W) $$
三つの負荷ですので、3倍になります。
$$ P_{\sum} = P\times3 = 9600(W) = 9.6(kW) $$
解答
ハ です。
一言:
三相回路ですので、3倍を忘れないでください。
デルタ(Δ)と星(★)結線図計算方を覚えてください。
今日の令和5年度上期一般問題(3)を終わらせていただきます。
ありがとうございました。

