ラプラス変換
皆さん、こんにちは。
本日は、ラプラス変換について復習いたします。
1.定義
ラプラス変換とは時間関数tからなる回路方程式(微分方程式)を解くために、数学的操作を加えて別の関数(s関数)に変換し、s関数総合間の関係として計算し、その計算結果をラプラス逆変換という数学的操作によりt関数に戻して答えを知ろうというものです。
2.公式
ラプラス変換:F(s) = ℒ{ f(t )}=∫_0^∞▒〖f(t)〗 ε^(-st)dt
ラプラス逆変換:f(t ) = L^(-1){F(s)} = 1/2πj ∫_(c-j∞)^(c+j∞)▒〖F(s)〗 ε^stds
3.電気回路における素子ラプラス変換公式
電圧:F(s) = ∫_0^∞▒〖f(t)〗 ε^(-st)dt = ∫_0^∞▒E ε^(-st)dt = (-E)/s ε^(-st) = E/s
抵抗:F(s) = ∫_0^∞▒〖f(t)〗 ε^(-st)dt = ∫_0^∞▒〖Ri(t)〗 ε^(-st)dt = R I(s)
コイル:F(s) = ∫_0^∞▒〖f(t)〗 ε^(-st)dt = ∫_0^∞▒L di/dt ε^(-st) dt = LI(s)
キャパシター:F(s) = ∫_0^∞▒〖f(t)〗 ε^(-st)dt = 1/C ∫_0^∞▒∫1▒〖i(t)ε^(-st) dt〗= I(s)/Cs
4.例
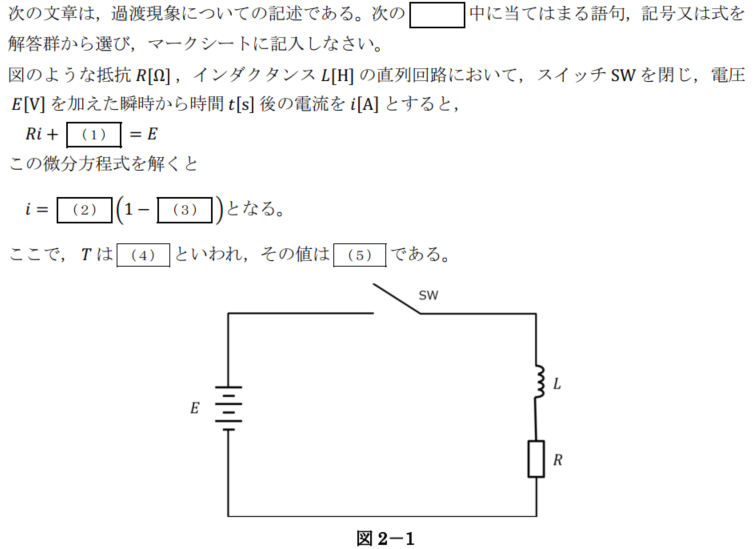
回路には電圧E、抵抗RとコイルLがあります。
まず、オームの法則通りに:Ri(t) + L di/dt = E (1)
次は、上の公式を使ったら、次のオームの法則を書けます: E/s = R I(s) + L sI(s)
⇔ E = s I(s) {Ls + R}⇒ I(s) = E/ L{s( s + R/L )} = E/L {L/Rs - L/R( s + R/L)}
逆ラプラス変換すると:i(t) E/L*L/R { 1 - ε^(-Rt/L)} = E/R{ 1 - ε^(-Rt/L)} = E/R{ 1 - ε^(-t/T)}
⇒ (2) = E/R, (3) = ε^(-t/T)。
このTは (4) 時定数といわれ、その値は(5) T = L/Rである。

