過度現象(2)
今日は、RC回路の過度現象を学習続きます。
RC回路
まず、回路にある素子を確認します。
右の回路のように、直流電源E、抵抗R、キャパシターCからなるRC回路です。
スイッチは、a,b位置をそれぞれ切り替わるときの電流、電圧などを求める。
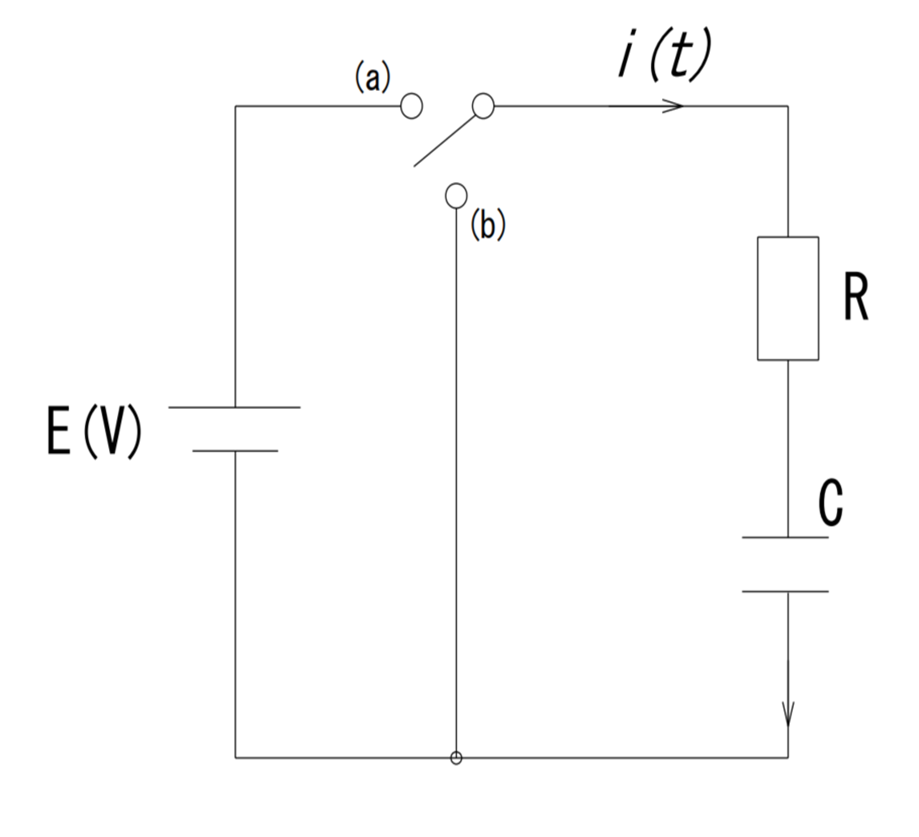
a位置に閉じる場合
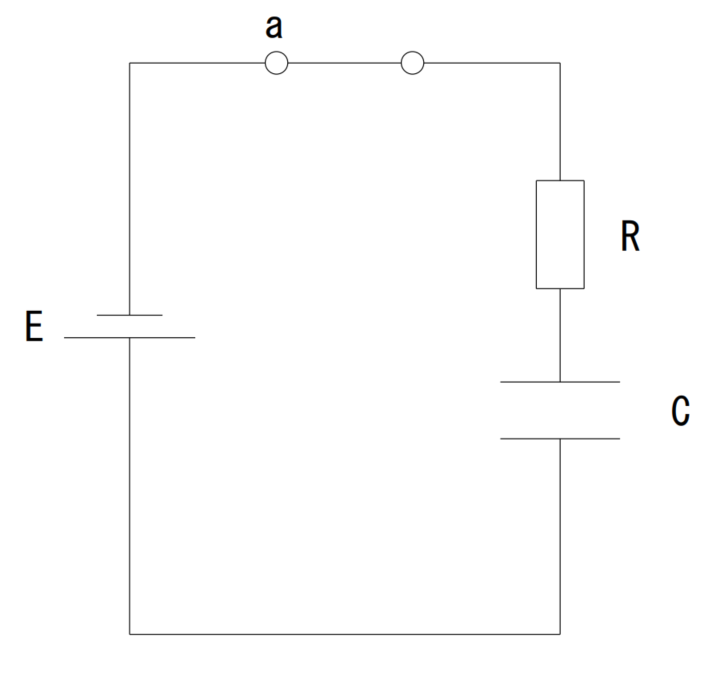
スイッチはa位置に閉じるときの回路は、R、C素子を直流電源Eに電圧を加えてもらえる。
この時の微分方程式を書けば
•RI(t)+1/C ∫1▒i(t)dt=E
初期条件は:i(0)=0をとして、ラプラス変換する。
•RI(s)+I(s)/Cs=E/s ⇒ I(s){R+1/Cs}=E/s
•I(s){RCs+1}=CsE/s=CE
•I(s)RC{s+1/RC}=CE ⇒ I(s)=E/R(1/(s+1/RC))
•I(t)=E/R (e^(-t/RC) ) (A)
•Vc(s)=I(s)/Cs=E/RC/{s(s+1/RC)}
•Vc(s)=E/RC RC{1/s-1/(s+1/RC)} ⇒ Vc(t)=E {1-e^(-t/RC)}
•※定常状態ではI(t)=0,Vc(t)=E
つまり、定常状態では、キャパシターに電荷を積んで、エネルギーを蓄える。
b位置に閉じる場合
今、直流電源を回路から取り外して、スイッチがa位置に閉じるときのキャパシターに蓄えたエネルギーを放電して、微分方程式が成り立ちます:
•Vr+Vc=0
今、直流電源を回路から取り外して、スイッチがa位置に閉じるときのキャパシターに蓄えたエネルギーを放電して、微分方程式が成り立ちます:
•Vr+Vc=0
•RI(t)+1/C ∫1▒i(t)dt+E=0
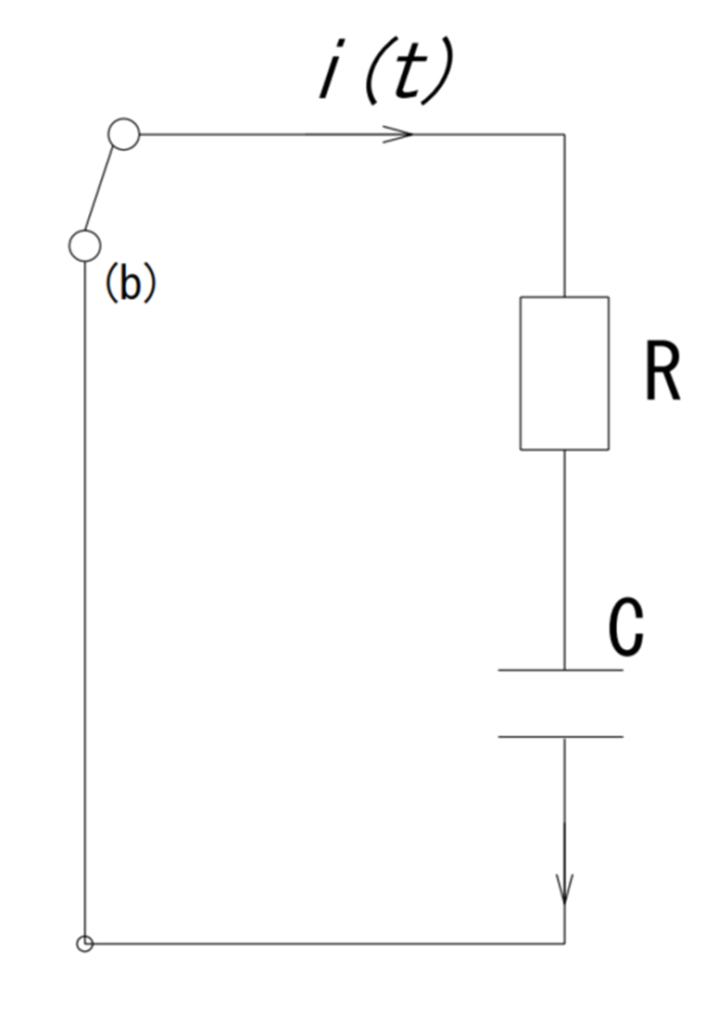
•I(0)=0,Vc(0)=Eの初期条件を使って、ラプラス変換進んでいく。
•RI(s)+I(s)/Cs-E/s=0
I(s){R+1/Cs}=E/s
I(s){R(s+1/RC)}=E⇒I(s)=E/R {1/(s+1/RC)}
•I(t)=E/R e^(-t/RC) (A)
Vc(s)=I(s)/Cs-E/Rs=E/RCs {1/(s+1/RC)}-E/Rs
=E/RC {RC(1/s-1/(s+1/RC))}-E/Rs=E {1/s-1/(s+1/RC)}-E/Rs
•=E(1/(s+1/RC))
•Vc(t)=E(e^(-t/RC) ) (V)
•※定常状態ではVc(t)=0
ここで、キャパシターに蓄えたエネルギーをすべて放電しましたので、電圧は零になることはわかる。

