第2種電気工事士学科試験問題シリーズ(2)
皆さんこんにちは!タンです。
今日は令和5年度上期一般問題を続けます。
問題2:
![問題2:抵抗率ρ[Ω・m]、直径D[mm]、長さL[m]の銅線の電気抵抗[Ω]を表す式は。](https://sdplanet.co.jp/wpt/wp-content/uploads/2023/09/20230922than01.png)
解答:
この問題は、抵抗の問題です、電気の基礎ですので、覚えてください。
導線の電気抵抗R(Ω):
ρ:低効率(Ω・m)
L:長さ(m)
S : 導線面積(㎡)
又は
$$ S = πr^2 \times 10^{-6} = π\frac{D^2}{4} \times 10^{-6} (m^2 ) $$
D : 導線直径(mm)
r : 導線半径(mm)
ので、
$$ R = ρ \frac{L}{S} = \frac{4ρL}{πD^2} \times 10^6 (Ω) $$
$$ R = ρ \frac{L}{S}(Ω) $$
解答
イ です。
一言:
単位に注意してください、例えば、長さL(m)、導線半径r、直径D(m)です。
電気抵抗と磁気抵抗を間違いないように、
磁気抵抗
$$ R_m = \frac{L}{μS} $$
、μ:透磁率。
つぎ、問題3:
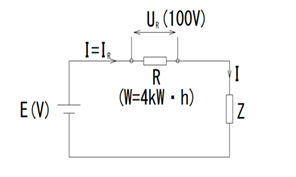
![抵抗に100Vの電圧を2時間30分加えたとき、電力量が4kW・hであった。抵抗に流れる電流[A]は。](https://sdplanet.co.jp/wpt/wp-content/uploads/2023/09/20230922than02.png)
解答:
抵抗に関する問題ですね、
時間(t)の間に抵抗で消費電力は
$$ W= U \times I \times t (J)$$
ので、
$$ I= \frac{W}{Ut} (A) $$
W : 電力 (J=W・s), (J=W・h)
U : 抵抗の端末電圧(V)
I : 抵抗に流れる電流(A)
t : 時間(s),(h)
問題により、
t = 2h30分=2.5(h)
W = 4kW・h = 4000 (W・h)
U = 100(V)
ので、
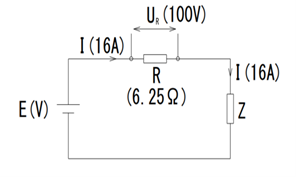
$$ I= \frac{W}{Ut} = \frac{4000}{100 \times 2.5} = 16(A)$$
解答
イ です。
一言:
電圧を注意してください、計算に使う電圧は、電源電圧(E)ではなくて、抵抗電圧(U)です。
ちなみに、この問題では、抵抗値計算なら、
$$ R = \frac{U}{I} = \frac{100}{16} = 6.25(Ω) $$
別の計算方:
$$ R = \frac{U^2t}{W} = \frac{100 \times 100 \times 2.5}{4000} = 6.25(Ω) $$
では、今日の内容を見ていただき、誠にありがとうございました。

